




Next: Module HiStats
Up: Module TArray
Previous: Working with sub-arrays and
Contents
Index
TArray T
T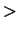 can handle numerical arrays with various memory
organisation, as long as the spacing (steps) along each axis is
regular. The five axis are labeled X,Y,Z,T,U. The examples below
illustrates the memory location for a 2-dimensional,
can handle numerical arrays with various memory
organisation, as long as the spacing (steps) along each axis is
regular. The five axis are labeled X,Y,Z,T,U. The examples below
illustrates the memory location for a 2-dimensional,
 .
The first index is along the X axis and the second index along the Y axis.
.
The first index is along the X axis and the second index along the Y axis.
| (0,0) (0,1) (0,2) (0,3) |
| (1,0) (1,1) (1,2) (1,3) |
| (2,0) (2,1) (2,2) (2,3) |
In the first case, the array is completely packed
(
 ), with zero offset,
while in the second case,
), with zero offset,
while in the second case,
 :
:
| 0 1 2 3 | | 10 12 14 16 |
Ex1 | 4 5 6 7 | Ex2 | 20 22 24 26 |
| 8 9 10 11 | | 30 32 34 36 |
For matrices and vectors, an optional argument ( MemoryMapping)
can be used to select the memory mapping, where two basic schemes
are available:
CMemoryMapping and FortranMemoryMapping.
In the case where CMemoryMapping is used, a given matrix line
is packed in memory, while the columns are packed when
FortranMemoryMapping is used. The first index when addressing
the matrix elements (line number index) runs along
the Y-axis if CMemoryMapping is used, and along the X-axis
in the case of FortranMemoryMapping.
Arithmetic operations between matrices
with different memory organisation is allowed as long as
the two matrices have the same sizes (Number of rows and columns).
The following code example and the corresponding output illustrates
these two memory mappings. The TMatrix T
T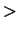 ::TransposeSelf()
method changes effectively the matrix memory mapping, which is also
the case of TMatrix
::TransposeSelf()
method changes effectively the matrix memory mapping, which is also
the case of TMatrix T
T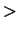 ::Transpose() method without argument.
::Transpose() method without argument.
TArray<r_4> X(4,2);
X = RegularSequence(1,1);
cout << "Array X= " << X << endl;
TMatrix<r_4> X_C(X, true, BaseArray::CMemoryMapping);
cout << "Matrix X_C (CMemoryMapping) = " << X_C << endl;
TMatrix<r_4> X_F(X, true, BaseArray::FortranMemoryMapping);
cout << "Matrix X_F (FortranMemoryMapping) = " << X_F << endl;
This code would produce the following output (X_F = Transpose(X_C)) :
Array X=
--- TArray<f> ND=2 SizeX*Y*...= 4x2 ---
1, 2, 3, 4
5, 6, 7, 8
Matrix X_C (CMemoryMapping) =
--- TMatrix<f>(NRows=2, NCols=4) ND=2 SizeX*Y*...= 4x2 ---
1, 2, 3, 4
5, 6, 7, 8
Matrix X_F (FortranMemoryMapping) =
--- TMatrix<f>(NRows=4, NCols=2) ND=2 SizeX*Y*...= 4x2 ---
1, 5
2, 6
3, 7
4, 8





Next: Module HiStats
Up: Module TArray
Previous: Working with sub-arrays and
Contents
Index
Reza Ansari
2001-03-07